こちらのサイトを利用してPython (Anaconda) でデータ解析の勉強をさせてもらおうと思います。
ハンバーガー統計学にようこそ!
import pandas as pd
url = 'http://kogolab.chillout.jp/elearn/hamburger/chap2/sec4.html'
dframe_list = pd.io.html.read_html(url, encoding="sjis")
from pandas import DataFrame
grade_data = dframe_list[0]
grade_data
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1 |
568 |
530 |
581 |
554 |
536 |
518 |
564 |
552 |
grade_data.drop([0])
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
568 |
530 |
581 |
554 |
536 |
518 |
564 |
552 |
import numpy as np
# チキンの重さ
# 数値の配列に変換
num_list =[ int(i) for i in grade_data.ix[1] ]
# 平均
mean_val = np.mean(num_list)
print('チキンの重さの解析結果')
print('平均= {}'.format(mean_val))
#print('標準偏差= {}'.format(num_std))
#print('分散= {}'.format(num__var))
# 2.2 母集団の平均と分散を推定する
# 不偏分散=((データ-平均値)の二乗)の総和÷(個数-1)
# (各データ-平均)の二乗を配列で作る
X = [ (int(i)-mean_val)**2 for i in grade_data.ix[1] ]
# 不偏分散を作る
fvar = np.sum(X) / (len(X)- 1)
print('不偏分散= {}'.format(fvar))
import matplotlib.pyplot as plt
%matplotlib inline
# t分布のインポート
from scipy.stats import t, sem
import numpy as np
# SEMは標準偏差をサンプル数Nのルートで割ったもの
sem_val = sem(num_list)
print('標本標準誤差= {}'.format(sem_val))
alpha = 0.95
ci = t.interval(alpha, len(num_list)-1, loc=mean_val, scale=sem_val)
print('95%確率信頼区間= {} 〜 {}'.format(ci[0], ci[1]))
alpha = 0.99
ci = t.interval(alpha, len(num_list)-1, loc=mean_val, scale=sem_val)
print('99%確率信頼区間= {} 〜 {}'.format(ci[0], ci[1]))
チキンの重さの解析結果
平均= 550.375
不偏分散= 445.69642857142856
標本標準誤差= 7.464050748181484
95%確率信頼区間= 532.7253245900785 〜 568.0246754099215
99%確率信頼区間= 524.2546790761623 〜 576.4953209238377
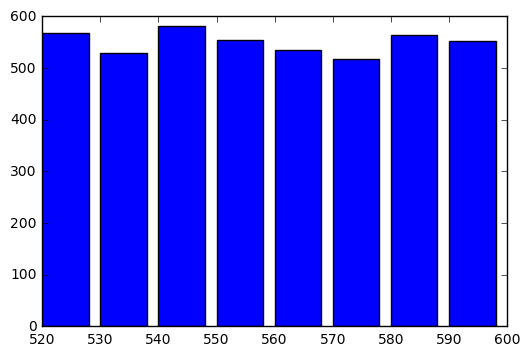
import matplotlib.pyplot as plt
# 横軸
x = [520,530,540,550,560,570,580,590]
# 棒グラフ
plt.bar(x, num_list, width=8)
<Container object of 8 artists>