「ハンバーガー統計学にようこそ!」をPythonでお勉強 4.4まで

こちらのサイトを利用してPython (Anaconda) でデータ解析の勉強をさせてもらおうと思います。
ハンバーガー統計学にようこそ!
4.4 実践編:ポテトの評価は?
import pandas as pd
url='http://kogolab.chillout.jp/elearn/hamburger/chap4/sec4.html'
dframe_list = pd.io.html.read_html(url, encoding="sjis")
#df = dframe_list[0]
df = grade_data
len(df)
nofloat = []
for i in range(len(df)):
try:
print(df.ix[:,i])
df.ix[:,i]=df.ix[:,i].astype(float)
except:
nofloat.append(i)
print('float convert Error', i)
df.ix[1][3] + df.ix[1][1]
type(df.ix[1][3])
1 1.0
2 2.0
3 3.0
4 4.0
5 5.0
6 6.0
7 7.0
8 8.0
Name: 0, dtype: float64
1 80.0
2 75.0
3 80.0
4 95.0
5 90.0
6 80.0
7 85.0
8 90.0
Name: 1, dtype: float64
1 1.0
2 2.0
3 3.0
4 4.0
5 5.0
6 6.0
7 7.0
8 8.0
Name: 2, dtype: float64
1 75.0
2 65.0
3 80.0
4 85.0
5 75.0
6 80.0
7 80.0
8 70.0
Name: 3, dtype: float64
float convert Error 4
float convert Error 5
float convert Error 6
float convert Error 7
numpy.float64
まず、帰無仮説を立てます。
帰無仮説:(未)
次に、その逆である対立仮説を立てます。
対立仮説:(未)
df.columns = ['ワクワクポテトを食べた女子高生','ワクワクの点数', 'モグモグポテトを食べた女子高生', 'モグモグの点数']
df
| ワクワクポテトを食べた女子高生 | ワクワクの点数 | モグモグポテトを食べた女子高生 | モグモグの点数 | |
|---|---|---|---|---|
| 1 | 1.0 | 80.0 | 1.0 | 75.0 |
| 2 | 2.0 | 75.0 | 2.0 | 65.0 |
| 3 | 3.0 | 80.0 | 3.0 | 80.0 |
| 4 | 4.0 | 95.0 | 4.0 | 85.0 |
| 5 | 5.0 | 90.0 | 5.0 | 75.0 |
| 6 | 6.0 | 80.0 | 6.0 | 80.0 |
| 7 | 7.0 | 85.0 | 7.0 | 80.0 |
| 8 | 8.0 | 90.0 | 8.0 | 70.0 |
import numpy as np
# ワクワクの平均
waku_mean_val = np.mean(df['ワクワクの点数'])
waku_std = np.std(df['ワクワクの点数'])
waku_var = np.var(df['ワクワクの点数'])
print("ワクワクの平均 = {}".format(waku_mean_val))
print("ワクワクの標準偏差 = {}".format(waku_std))
print("ワクワクの分散 = {}".format(waku_var))
# モグモグの平均
mogu_mean_val = np.mean(df['モグモグの点数'])
mogu_std = np.std(df['モグモグの点数'])
mogu_var = np.var(df['モグモグの点数'])
print("モグモグの平均 = {}".format(mogu_mean_val))
print("ワクワクの標準偏差 = {}".format(mogu_std))
print("ワクワクの分散 = {}".format(mogu_var))
ワクワクの平均 = 84.375
ワクワクの標準偏差 = 6.343057228182637
ワクワクの分散 = 40.234375
モグモグの平均 = 76.25
ワクワクの標準偏差 = 5.994789404140899
ワクワクの分散 = 35.9375
# 自由度を求める
# サンプル数
waku_count = len(df['ワクワクの点数'])
mogu_count = len(df['モグモグの点数'])
# 自由度を計算
degree_of_freedom = (waku_count - 1) + (mogu_count - 1)
print("自由度 = {}".format(degree_of_freedom))
自由度 = 14
# tを求める
# t=(標本平均の差)/(差の標本標準誤差)
import math
# 標本平均の差
_mean_val = mogu_mean_val - waku_mean_val
print("標本平均の差 = {}".format(_mean_val))
# 推定母分散
_var = ( (waku_var * waku_count) + (mogu_var * mogu_count) ) / ( (waku_count - 1) + (mogu_count - 1) )
print("推定母分散 = {}".format(_var))
# 差の標本標準誤差
_margin = math.sqrt( _var * (1/waku_count + 1/mogu_count) )
print("差の標本標準誤差 = {}".format(_margin))
it = _mean_val / _margin
print("it = {}".format(it))
標本平均の差 = -8.125
推定母分散 = 43.526785714285715
差の標本標準誤差 = 3.2987416431984227
it = -2.463060426921489
t_data = dframe_list[2].drop([0])
t_data.columns = ["自由度", "有意水準5%", "有意水準1%"]
t_data
| 自由度 | 有意水準5% | 有意水準1% | |
|---|---|---|---|
| 1 | 1 | 12.706 | 63.657 |
| 2 | 2 | 4.303 | 9.925 |
| 3 | 3 | 3.182 | 5.841 |
| 4 | 4 | 2.776 | 4.604 |
| 5 | 5 | 2.571 | 4.032 |
| 6 | 6 | 2.447 | 3.707 |
| 7 | 7 | 2.365 | 3.499 |
| 8 | 8 | 2.306 | 3.355 |
| 9 | 9 | 2.262 | 3.250 |
| 10 | 10 | 2.226 | 3.169 |
| 11 | 11 | 2.201 | 3.106 |
| 12 | 12 | 2.179 | 3.055 |
| 13 | 13 | 2.160 | 3.021 |
| 14 | 14 | 2.145 | 2.977 |
| 15 | 15 | 2.131 | 2.947 |
| 16 | 16 | 2.120 | 2.921 |
| 17 | 17 | 2.110 | 2.898 |
| 18 | 18 | 2.101 | 2.878 |
| 19 | 19 | 2.093 | 2.861 |
| 20 | 20 | 2.086 | 2.845 |
| 21 | 21 | 2.080 | 2.831 |
| 22 | 22 | 2.074 | 2.819 |
| 23 | 23 | 2.069 | 2.807 |
| 24 | 24 | 2.064 | 2.797 |
| 25 | 25 | 2.060 | 2.787 |
| 26 | 26 | 2.056 | 2.779 |
| 27 | 27 | 2.052 | 2.771 |
| 28 | 28 | 2.048 | 2.763 |
| 29 | 29 | 2.045 | 2.756 |
| 30 | 30 | 2.042 | 2.750 |
| 31 | 40 | 2.021 | 2.704 |
| 32 | 60 | 2.000 | 2.660 |
| 33 | 120 | 1.980 | 2.617 |
| 34 | ∞ | 1.960 | 2.576 |
# 有意水準は5%という条件なので
print("5%の列の自由度 = {}".format(t_data['有意水準5%'].ix[degree_of_freedom]))
5%の列の自由度 = 2.145
from scipy.stats import t
x = np.linspace(-5,5,100)
import matplotlib.pyplot as plt
%matplotlib inline
rv = t(degree_of_freedom)
print("自由度14のt分布")
plt.plot(x, rv.pdf(x))
自由度14のt分布
[<matplotlib.lines.Line2D at 0x1132b1940>]
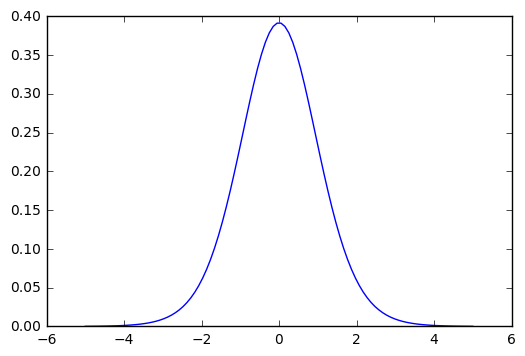
it(=2.463) > t(=2.145)なので仮説は棄却・・・だと思うけどこの辺の考え方はもっと勉強しなければいまいちピンとこないな・・・。

