「ハンバーガー統計学にようこそ!」をPythonでお勉強 1.9まで

こちらのサイトを利用してPython (Anaconda) でデータ解析の勉強をさせてもらおうと思います。
ハンバーガー統計学にようこそ!
今日は1.9 通過テストから
データを持ってきます。
# 1.9 通過テスト
import pandas as pd
url = 'http://kogolab.chillout.jp/elearn/hamburger/chap1/sec9.html'
dframe_list = pd.io.html.read_html(url, encoding="sjis")
from pandas import DataFrame
grade_data = dframe_list[0]
grade_data
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 学生番号 | 桜組 | 桃組 | 柳組 |
| 1 | 1 | 78 | 70 | 57 |
| 2 | 2 | 62 | 72 | 59 |
| 3 | 3 | 81 | 68 | 55 |
| 4 | 4 | 59 | 75 | 62 |
| 5 | 5 | 72 | 65 | 52 |
| 6 | 6 | 68 | 71 | 58 |
| 7 | 7 | 75 | 69 | 56 |
| 8 | 8 | 65 | 76 | 63 |
| 9 | 9 | 80 | 64 | 51 |
| 10 | 10 | 60 | 80 | 67 |
| 11 | 11 | 78 | 60 | 47 |
| 12 | 12 | 62 | 73 | 60 |
| 13 | 13 | 70 | 67 | 54 |
grade_data.columns = ["学生番号","桜組","桃組","柳組"]
grade_data.drop([0])
| 学生番号 | 桜組 | 桃組 | 柳組 | |
|---|---|---|---|---|
| 1 | 1 | 78 | 70 | 57 |
| 2 | 2 | 62 | 72 | 59 |
| 3 | 3 | 81 | 68 | 55 |
| 4 | 4 | 59 | 75 | 62 |
| 5 | 5 | 72 | 65 | 52 |
| 6 | 6 | 68 | 71 | 58 |
| 7 | 7 | 75 | 69 | 56 |
| 8 | 8 | 65 | 76 | 63 |
| 9 | 9 | 80 | 64 | 51 |
| 10 | 10 | 60 | 80 | 67 |
| 11 | 11 | 78 | 60 | 47 |
| 12 | 12 | 62 | 73 | 60 |
| 13 | 13 | 70 | 67 | 54 |
from scipy.stats import randint
import numpy as np
# 桜組の分散や標準偏差
sakura_list = [ int(i) for i in grade_data.drop([0])["桜組"] ]
sakura_low = min(sakura_list)
sakura_high = max(sakura_list)
sakura_mean, sakura_var = randint.stats( sakura_low, sakura_high )
sakura_std = np.std(sakura_list)
sakura__var = np.var(sakura_list)
print('桜組の解析結果')
print('平均= {} 分散={}'.format(sakura_mean, sakura_var))
print('標準偏差= {}'.format(sakura_std))
print('分散= {}'.format(sakura__var))
桜組の解析結果
平均= 69.5 分散=40.25
標準偏差= 7.62586691162691
分散= 58.15384615384615
# 桃組の分散や標準偏差
momo_list = [ int(i) for i in grade_data.drop([0])["桃組"] ]
momo_low = min(momo_list)
momo_high = max(momo_list)
momo_mean, momo_var = randint.stats( momo_low, momo_high )
momo_std = np.std(momo_list)
momo__var = np.var(momo_list)
print('桃組の解析結果')
print('平均= {} 分散={}'.format(momo_mean, momo_var))
print('標準偏差= {}'.format(momo_std))
print('分散= {}'.format(momo__var))
桃組の解析結果
平均= 69.5 分散=33.25
標準偏差= 5.188745216627709
分散= 26.923076923076923
# 柳組の分散や標準偏差
yanagi_list = [ int(i) for i in grade_data.drop([0])["柳組"] ]
yanagi_low = min(yanagi_list)
yanagi_high = max(yanagi_list)
yanagi_mean, yanagi_var = randint.stats( yanagi_low, yanagi_high )
yanagi_std = np.std(yanagi_list)
yanagi__var = np.var(yanagi_list)
print('柳組の解析結果')
print('平均= {} 分散={}'.format(yanagi_mean, yanagi_var))
print('標準偏差= {}'.format(yanagi_std))
print('分散= {}'.format(yanagi__var))
柳組の解析結果
平均= 56.5 分散=33.25
標準偏差= 5.188745216627709
分散= 26.923076923076923
import seaborn as sns
%matplotlib inline
# ヒストグラムとカーネル密度推定を描く
sns.distplot(sakura_list,bins=8, color='r')
sns.distplot(momo_list,bins=8, color='b')
sns.distplot(yanagi_list,bins=8, color='g')
//anaconda/lib/python3.5/site-packages/statsmodels/nonparametric/kdetools.py:20: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
y = X[:m/2+1] + np.r_[0,X[m/2+1:],0]*1j
<matplotlib.axes._subplots.AxesSubplot at 0x1134c0ac8>
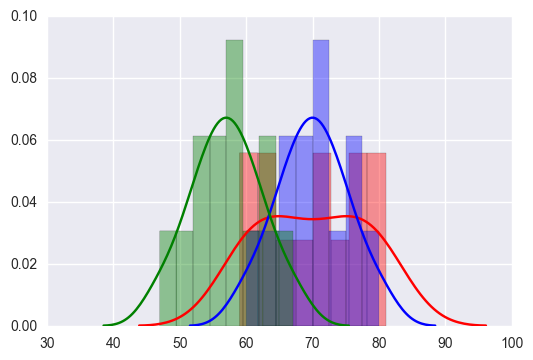
考察
- 桜組 赤
- 桃組 青
- 柳組 緑
桜組は実力に抜けた人は居ない。
桜組は実力差が他に比べて大きい。
桃・柳は標準偏差が同じだったがクラスとしての実力レベルは桃組が高い。
こういった感じでいいのかな・・・?



